Az első félév lezárult, most szünet van már egy hete. Múlt hét szerdán volt az osztályozó értekezlet mindkét iskolámban, de mivel hivatalosan riedenburgos vagyok, ott kellett jelen lennem. Igazából lement volna nélkülem is a dolog, mert a jegyeket már beírtam előzőleg a rendszerbe és rendkívüli esemény sem történt a félévben, de hát adni kell a formalitásokra is.
Összesen hat osztályom van az idén, három itt, három ott. Mindegyikben buktak félévkor, hol többen, hol kevesebben, annak ellenére, hogy akit csak lehetett, megmentettem. A Marienbergben például annyian kértek szóbeli javítóvizsgát az utolsó hétre, hogy szerda reggel a lyukasórámban is vizsgáztatnom kellett. Végül azért lement minden rendben, de a múlt hét előtti hét mozgalmas volt (múlt hét előtti pénteken zártuk ugyanis a jegyeket; az osztályozó értekezlet meg rákövetkező szerdán volt).
Korábban már írtam róla, hogy a gimnáziumi osztályom Casio Classpad II. típusú számológéppel fog érettségizni. Kölcsönkaptam egyet az egyik kollégától és még korábban és akkor már próbálgattam is hogy mit tud, de most egy kicsit jobban belementem és azt kell, hogy mondjam, sokat tud. Ez viszont kérdéseket is felvet azzal kapcsolatban, hogy mit tanítsak az osztálynak.
Most például épp az egyenlőtlenségekről tanulunk. A legfontosabb különbség az egyenletekhez képest, hogy ha az egyenlőtlenséget negatív számmal szorozzuk vagy osztjuk, akkor a relációjelet meg kell fordítani. Ez egy egyszerű szabály, de ha az egyenlőtlenségben olyan tört van, aminek a nevezőjében ismeretlen van, akkor az megbonyolítja a megoldást. Itt egy példa (az alaphalmaz a valós számok halmaza):
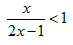
Az első lépés az, hogy megszorozzuk mindkét oldalt 2x – 1-gyel. Csak egy gond van: nem tudjuk, hogy x mekkora. Emiatt a 2x – 1 lehet pozitív vagy negatív is. Ha pedig negatív számmal szorzunk egy egyenlőtlenséget, akkor meg kell fordítani a relációjelet. Akkor most megfordítsuk vagy ne? Mivel nem lehetünk biztosak, hogy a 2x – 1 pozitív vagy negatív, ezért mindkét esetet végig kell számolnunk. A megoldást itt két esetre választjuk szét: az első esetben abból indulunk ki, hogy a 2x – 1 kifejezés pozitív, a második esetben ennek az ellenkezőjét tesszük fel, és megnézzük, hogy mi történik, ha a 2x – 1 negatív.
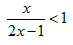
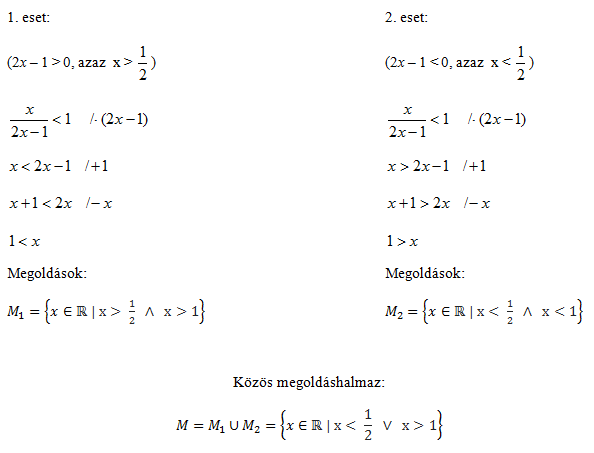
Végül is nem annyira bonyolult, de mire ezt mindenki megérti (és alkalmazni is tudja) az osztályban, elmegy vagy két óra. Nézzük meg ugyanezt az új számológéppel:
Mindennel együtt vagy negyven másodpercig tart egy ilyen egyenlőtlenséget megoldani. A solve-parancs használatát kell ismerni, a többi már könnyű. Bárki meg tudja tanulni tíz perc alatt.
Más műveletek, például a deriválás (ami itt az érettségi anyag része) is leegyszerűsödik egy ilyen számológéppel:
Talán most már érthetőbb, hogy milyen kérdéseket vet fel az új technológia. Bár még csak másfél éve tanítok, de már tapasztaltam, hogy az órák nagy részét az viszi el, hogy megmutatom és begyakoroltatom az osztállyal, hogy hogyan kell bizonyos problémákat megoldani - papíron. Az osztást, szorzást, gyökvonást és a hasonló műveletet számológéppel végezzük, de az egyes új témakörökhöz kapcsolódó lényegi elemeket a diákoknak meg kell tanulniuk és papíron csinálják. Például a másodfokú egyenleteket a másodfokú egyenlet megoldóképlete alapján oldottunk meg; hatványokat a hatványozás azonosságai alapján egyszerűsítettünk vagy írtunk át más alakra; exponenciális egyenleteket a logaritmus azonosságai alapján oldottunk meg. Mindegyikhez szükség van képletek, szabályok vagy eljárások ismeretére. Egy ilyen számológép birtokában viszont nem kell a hatványozás azonosságait tudni, mert a számológép úgyis megoldja a feladatot. Ugyanez érvényes az alapvetőbb dolgokra is, mint például a képletátalakítások vagy a törtek egyszerűsítése.
Ami a képletek és azonosságok ismeretét illeti, azokat úgyis csak az első két évben kell megtanulni, utána már használhatnak képletgyűjteményt, amiben úgyis minden benne van. Maradnak tehát a megoldási módszerek, eljárások ismeretei, amik ilyen technikai háttér mellett feleslegessé válnak. Ezt pozitívumként lehet értékelni, mert idő szabadul fel, amit az ember szöveges feladatok megoldására fordíthat, erre pedig szükség is van. A természetes nyelven megfogalmazott matematikai problémák szimbolizálása, azaz lefordítása számokra, egyenletekre vagy más hasonló kifejezésekre sok diáknak okoz gondot, ha tehát több idő marad erre a részre, az jó. Másrészről viszont úgy érzi az ember, hogy így kreatív gondolatok mennek veszendőbe, amiken sok megoldási módszer alapul. A középiskolai matematikatanulás értelme az érettségin túl épp az, hogy a logikus gondolkodás képességét fejlessze. A képleteket és a konkrét megoldási módszereket a többség az érettségi után elfelejti, mert nem használja; a logikus gondolkodás képessége - amit a matematika jól fejleszt - viszont marad (legalábbis ezt reméljük). Ezt képességet pedig fejleszti, ha bele kell gondolni, hogy hogyan oldok meg egy feladatot, mit tudok átvenni a már ismert megoldási módszerekből, és min kell változtatnom. Ennek egy része kiesik egy ilyen számológép mellett. Így is megvalósítható a logikus gondolkodás képességének fejlesztése, de bennem mégis van egy kis hiányérzet ezzel kapcsolatban, de lehet, hogy ez csak átmeneti állapot, ami a megszokásból adódik. Alapjában véve a kompetenciaalapú oktatás mellett vagyok: ha a diákok egyszer kikerülnek az iskolából, a munkahelyen is használhatnak majd számítógépet a problémamegoldáshoz; a lényeg az lesz, hogy a problémát jól tudják értelmezni, részekre bontani, és a megfelelő kérdéseket tegyék fel a gépnek.
Viszont: egy másik, ehhez kapcsolódó dolog a továbbtanulás kérdése. Ha valaki műszaki vagy természettudományos vonalon megy tovább, biztos, hogy kell még matematikát tanulnia. Ismerősöktől tudom, hogy - legalábbis bevezető matematikai tárgyaknál biztosan - előfordul, hogy az ember nem használhat számológépet a feladatok megoldásánál. Vagyis mégiscsak tisztában kell lenni mondjuk a deriválási szabályokkal vagy az abszolútértékes egyenletek megoldási módszereivel. Nem hiszem, hogy ez a gyakorlat gyorsan megváltozik. Ha viszont ez így van, akkor a tanárnak mégis tanítania kell megoldási módszereket is.
Ezen felül általában az is igaz, hogy ha az ember egy matematikai bizonyítást meg szeretne érteni, akkor a fent említett azonosságokkal tisztában kell lennie, különben nem fogja tudni követni, hogy mi történik. Egy bizonyításban ugyanis tipikusan az történik, hogy egy kiinduló állítást lépésről-lépésre addig alakítgatunk más alakra, amíg egyszer csak nyilvánvalóan látható lesz a bizonyítandó tételhez való viszonya. Bizonyításokat egyébként csak a legritkább esetben veszünk az órákon, mert érettségire nem kellenek. Én néha levezetek azért egy-egy tételt vagy azonosságot, mert az a véleményem, hogy a diákoknak a matematikának ezt az oldalát is ismerniük kell, nem csak a feladatmegoldásokat.
Visszatérve a továbbtanulás kérdéséhez: bonyolítja a helyzetet, hogy csak gimnáziumokban érettségiznek ilyen számológéppel a diákok, szakközépiskolákban olyan grafikus számológépet használnak (például TI-82 Stats-t), ami ugyan programozható, de alapból nem tud olyan bonyolult dolgokat megoldani, mint ez a Casio Classpad II. Ez azt jelenti, hogy aki szakközépiskolában érettségizik, annak mélyebb tudása lesz a megoldási eljárások terén és tőle joggal lesz elvárható egyetemen is, hogy ezeket számológép nélkül is tudja; a diákok másik felénél (azoknál, akik gimnáziumból mennek egyetemre) ez nem így lesz.
Az gimnáziumi osztályomban egyelőre még senkinek sincs ilyen Casio számológépe, úgyhogy még van idő, hogy tisztázzam ezeket a kérdéseket. Ha minden jól megy, majd talán május környékén viszont már mindenkinek lesz.