A múlt héten érdekes dolog történt a nyolcadikos gimnáziumi osztályomban, miközben a határozott integrálról tanultunk.
Írtam a témához egy általános összefoglalót, de minden érthető lesz enélkül is, ha a határozott integrál fogalma nem teljesen ismeretlen.
Összefoglalás (határozott integrál)
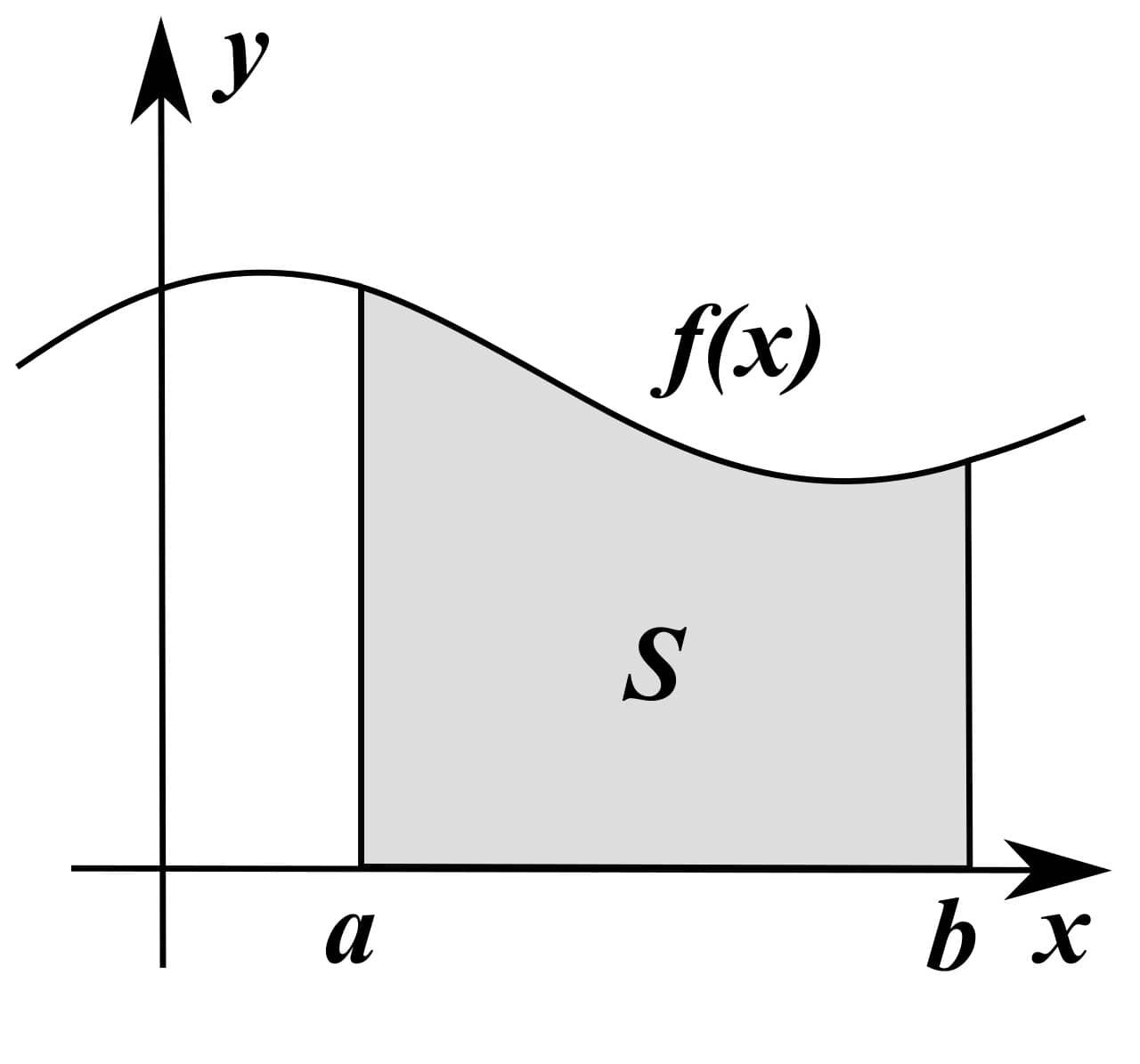Forrás: Von 4C - Eigenes Werk, based on JPG version, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=1039841 (2020.10.25)
Itt a függvénygörbét f(x) jelöli, az intervallum határai a és b, a közrezárt terület pedig S. Az integrálszámításban bevett írásmód alapján ezt a következőképpen lehet írni:
("integrál a-tól b-ig f(x) dx egyenlő S")
Bár a jobb számológépek tudnak hátrozott integrált számolni, ezt meg lehet csinálni papíron, ceruzával is. Röviden arról van szó, hogy az ember kiszámítja a megadott függvény ún. primitív függvényét, amit általában F-fel szokás jelölni. Ezután be kell helyettesíteni az intervallum felső határát a primitív függvénybe, majd az alsót, és a behelyettesítés után kijött első értékből ki kell vonni a másodikat:
(Ez az ún. Newton-Leibniz-tétel)
A területet azért nevezik előjelesnek, mert - az integrálszámítás sajátosságaiból adódóan - ha a vízszintes tengely felett van, pozitív az előjele, ha alatta, negatív. Ha részben felette, részben alatta van, akkor az előjeles területeket össze kell adni, az adja meg az integrál értékét az adott intervallumon.
Ebből az következik, hogy különbség lehet egy integrál értéke és az általa kijelölt terület nagysága között.
A következő képen az
függvény grafikonja látható, amit 0-tól 2-ig, valamint 2-től 3-ig integráltam.
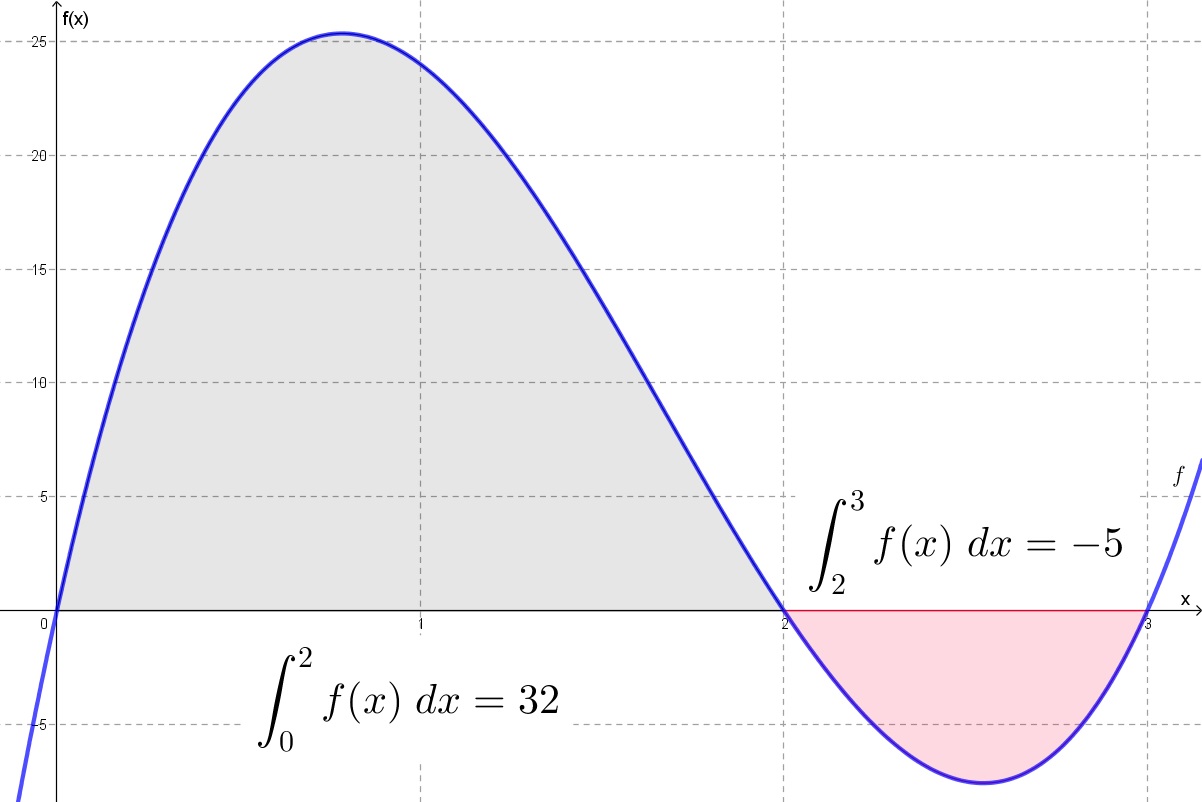
Az f függvény integrálja 0-tól 2-ig 32. Ez azt jelenti, hogy a függvény grafikonja és a vízszintes tengely közötti (a képen kékkel jelölt) terület a 0 és 2 által határolt intervallumon 32 négyzetegység nagyságú, és a vízszintes tengely felett van. Hasonlóan értelmezhető a másik, az ábrán pirossal jelölt területrész is, csak ott az integrálás eredménye negatív, mert a terület a vízszintes tengely alatt van.
A kék terület 32, a piros terület 5 négyzetegység nagyságú. A kettő összesen 37 négyzetegység.
Ha viszont az f függvényt 0-tól 3-ig integráljuk, azt kapjuk, hogy
ugyanis integrálás esetén az előjeles területek összeadódnak, ami ebben az esetben az jelenti, hogy a számítás módja 32 + (-5) = 32 - 5 = 27.
Ez elsőre furcsának tűnhet, de vannak összefüggések, ahol van értelme. Tegyük fel, hogy az f függvény egy egyenes mentén mozgó test sebességét írja le (az x az idő másodpercben, f(x) pedig a sebesség m/s-ban az x-edig időpillanatban). Ez azt jelenti például, hogy a test sebessége egy másodperc után 24 m/s (ez hozzávetőleg leolvasható az ábráról is).
A fizika törvényei alapján (ennek bizonyításába most nem megyek bele) függvénygörbe és a vízszintes tengely közötti terület a test által megtett út változását fejezi ki.
A grafikonról leolvasható, hogy a test sebessége a megfigyelés kezdetekor (= 0 másodperc) 0 m/s, azaz a test nem mozog. Ezután a sebesség egészen kb. 0,78 másodpercig növekszik, majd csökkenni kezd és két másodperccel a megfigyelés kezdete után megint 0, azaz a test ismét áll.
azt jelenti, hogy a test a megfigyelés első két másodperce alatt 32 métert tett meg a kiindulóponttól számítva. Az eredmény előjele azért pozitív, mert a kiindulóponthoz viszonyított pozitív irányban mozgott (ebbe az irányba távolodott a kiindulóponttól)
A második és harmadik másodperc között a függvénygörbe a vízszintes tengely alatt van, a függvényértékek is negatívak, vagyis a sebesség ebben az időintervallumban negatív, a test az ellenkező irányba halad, mint előzőleg.
tehát azt jelenti, hogy a test a második és harmadik másodperc között 5 méter utat tett meg a negatív irányban, ami ebben az esetben azt jelenti, hogy a test visszafelé, a kiindulópont irányába haladt.
A test tehát összesen 32 + 5 = 37 méter utat tett meg az első három másodpercben, de mivel ebből 32 méteren keresztül távolodott, aztán 5 méteren keresztül közeledett a kiindulóponthoz, így összesen 32 - 5 = 27 méter távolságban van tőle. Ezt a két dolgot integráljelek segítségével a következőképpen lehet írni:
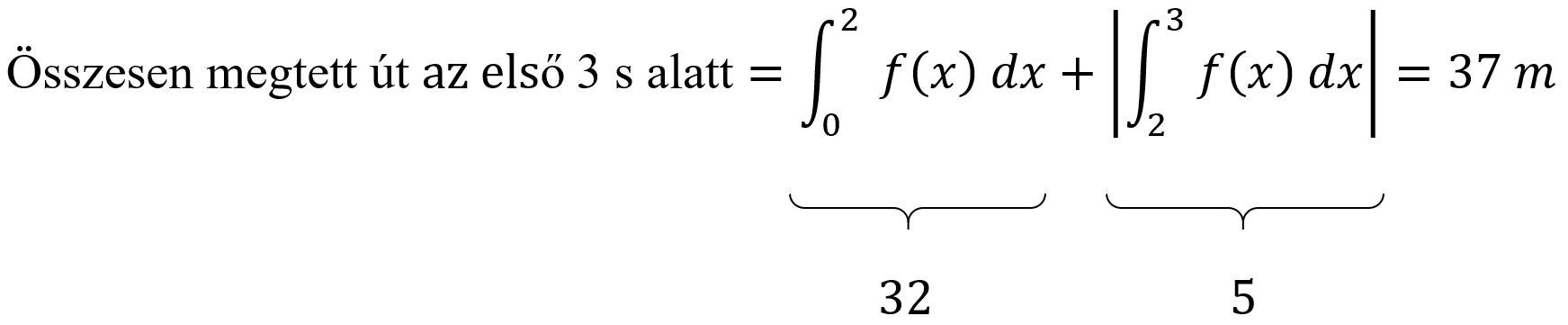
(az összeg második tagja azért van abszolútértékben, mert az összesen megtett út esetében nem érdekes, hogy melyik irányba tartott a test)
Röviden ezt jelenti tehát, hogy a határozott integrál segítségével egy [a;b] intervallumon kiszámítható a függvénygörbe és a vízszintes tengely közötti előjeles terület.
-----------------------------------------------------------------------
A téma elején, mint máskor is, lineáris függvényeket integráltunk. Az első feladat a következő volt:
Számítsd ki a határozott integrált a-tól b-ig 1) f-nek egy F primitív függvényével, 2) területképlet segítségével.
Koordináta-rendszerben ez így néz ki:
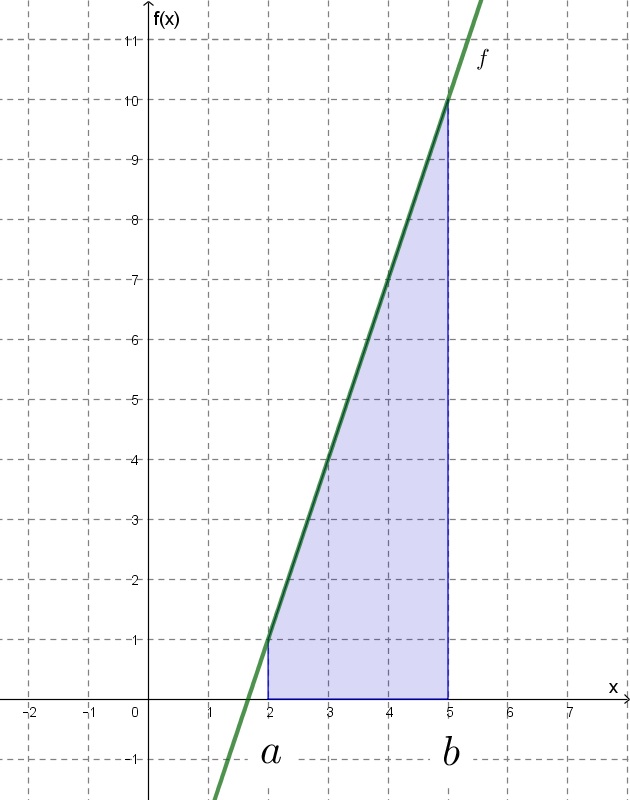
a1) Ennél a részfeladatnál az
értéket kell kiszámítani.
a2) Itt azt kell észrevenni, hogy a kiszámítandó terület egy derékszögű trapézhoz tartozik, és a trapéz területképletét kell felhasználni:
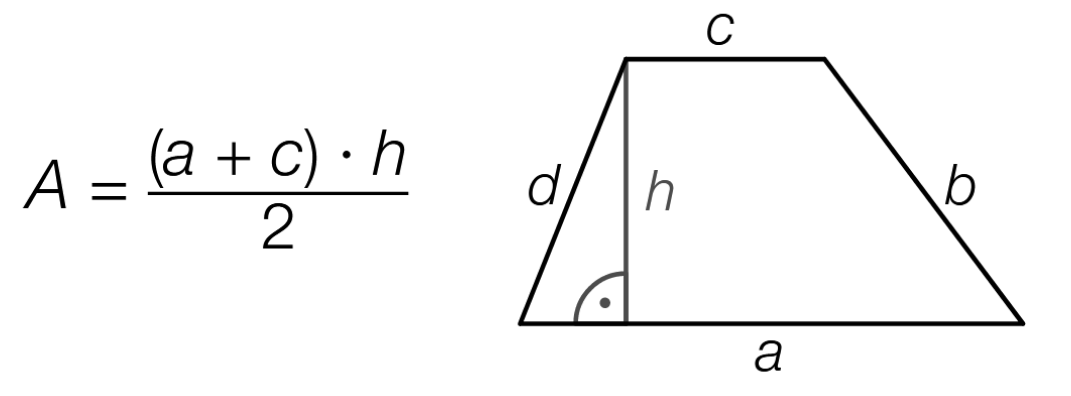
A feladatra alkalmazva:
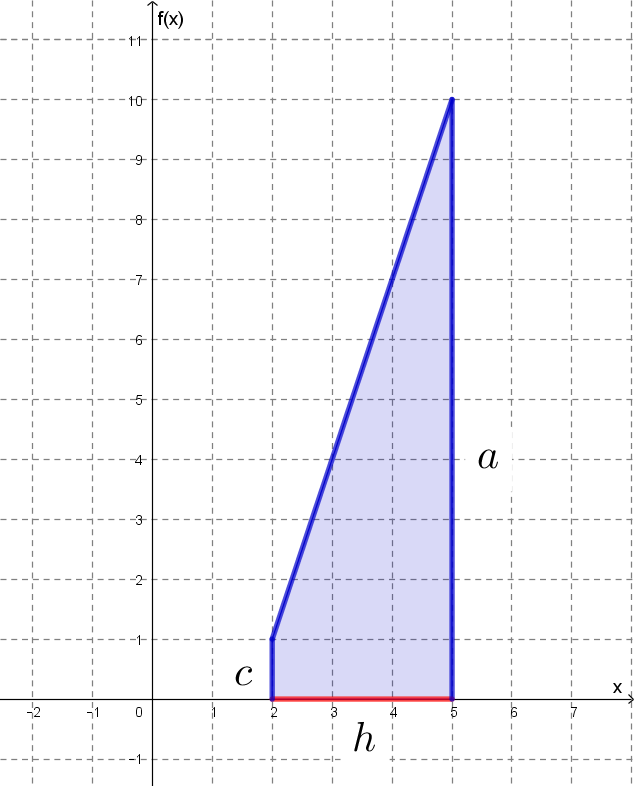
A kereset terület (itt A-val jelölve) tehát:
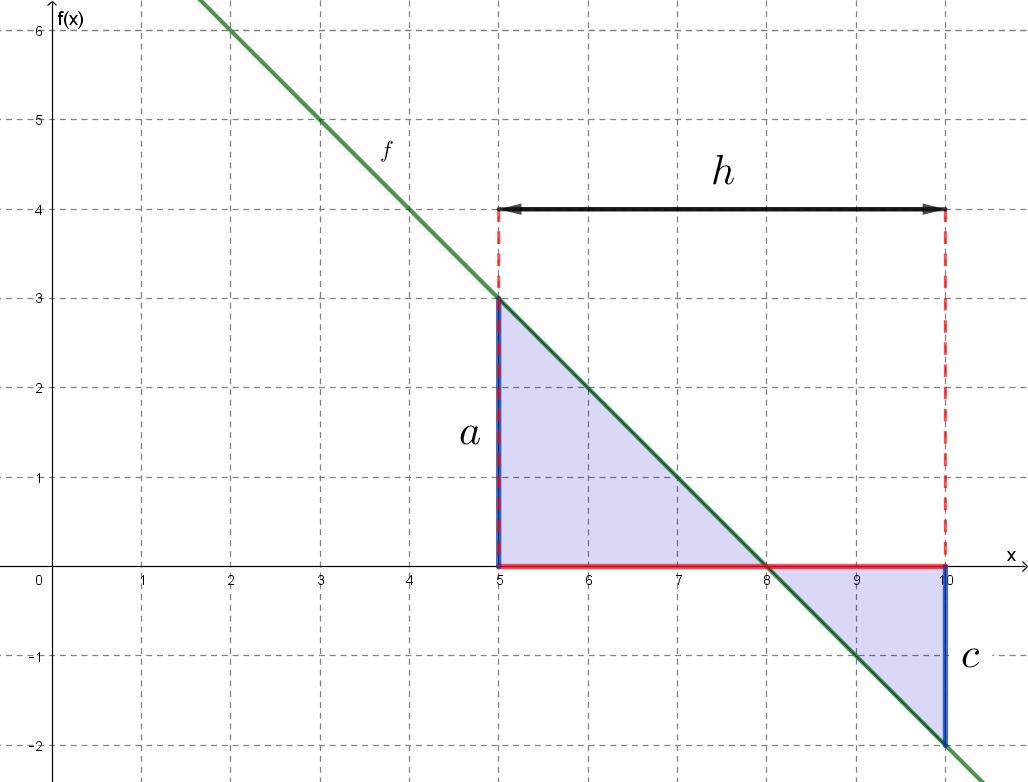
Az a) feladat volt a mintafeladat, amit a diákok bevonásával a táblánál számoltam végig. A b) feladatot mindenkinek önállóan vagy a padtárssal együtt, közös munkában kellett megoldani. A b) feladat olyan volt, mint az a), csak más függvénnyel és intervallummal:
Számítsd ki a határozott integrált a-tól b-ig 1) f-nek egy F primitív függvényével, 2) területképlet segítségével.
Koordináta-rendszerben:
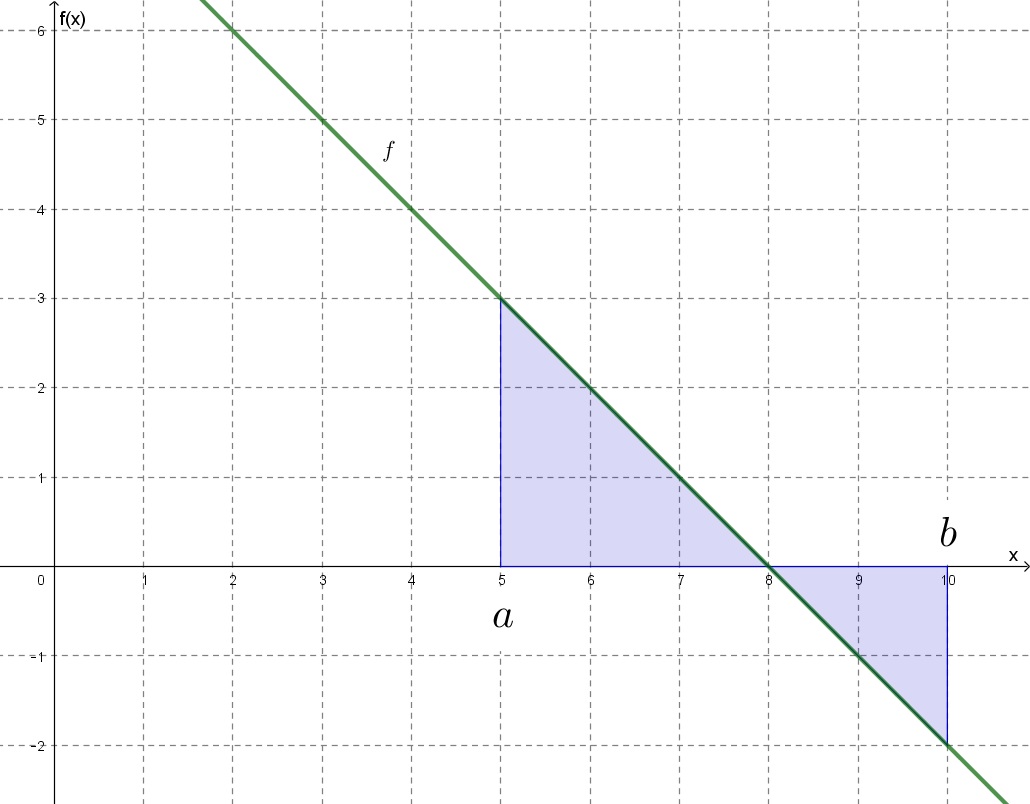
b1) A feladatot úgy kell megcsinálni, mint az előzőt, csak a kiindulási adatok mások:
b2) Az ilyen feladatot általában úgy szokás megoldani, hogy a két derékszögű háromszög területét kiszámolja az ember, aztán a vízszintes tengely feletti háromszög területéből kivonja a vízszintes tengely alattit.
Területképlet:
Ebben a feladatban ez így néz ki:
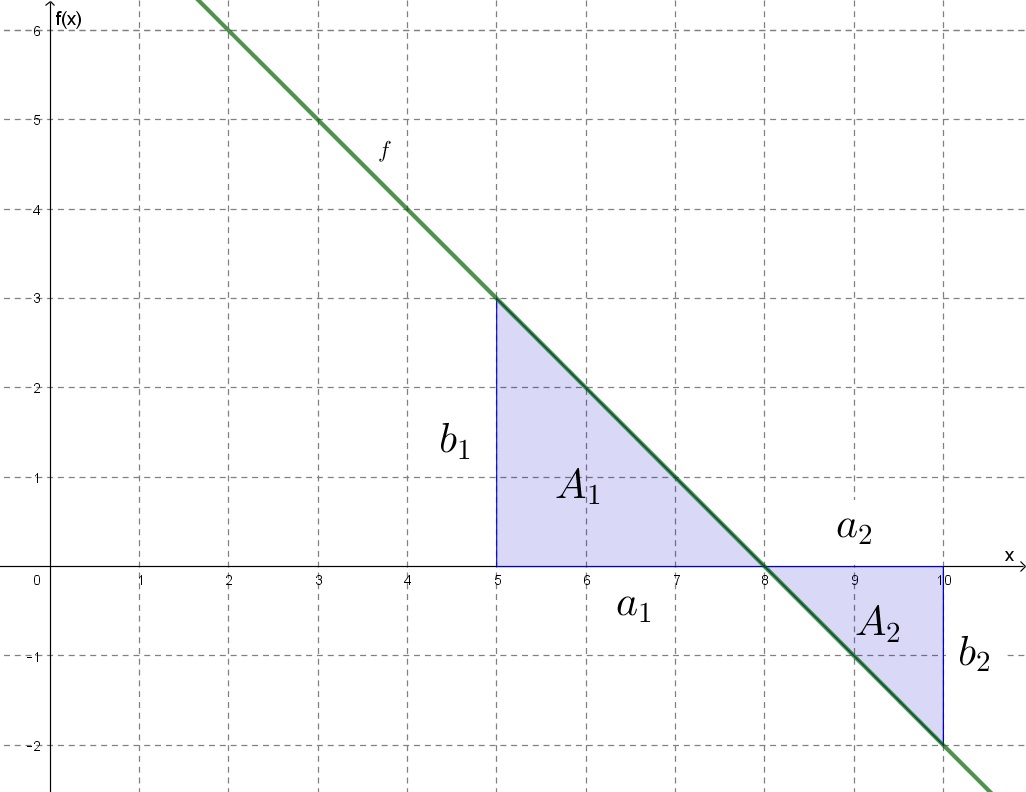
Képlet:
A legtöbben így is számoltak. Az egyik diák viszont az előző feladat mintájára szerencsét próbált a trapéz képletével és bejött neki, a helyes eredményt kapta. Így csinálta:
Képletbe helyettesítve:
A diák óra végén, a csengetéssel nagyjából egyidőben hozta oda a füzetét a tanári asztalhoz. Azt kérdezte, hogy mindig meg lehet-e oldani ezeket a feladatok így. Mivel sietnem kellett a másik órára (ilyenkor csak ötperces szünetek vannak), azt mondtam, hogy elsőre úgy látszik, hogy működik a módszere, de át kell gondolnom, hogy tényleg minden esetben így van-e. Aztán átmentem a hetedikes osztályba valószínűségszámítást tanítani, a kérdést pedig félretettem egy időre.
Aznap este az íróasztalnál ülve eszembe jutott a dolog és megkerestem a feladatot a tankönyvben.
Gondotam kipróbálok az eredeti feladatban megadotthoz képest más intervallumokat és más lineáris függvényeket is, hogy lássam, hogy mindig az jön-e ki, aminek ki kell jönnie. Az jött ki.
Megrajzoltam az egészet GeoGebrában is, hogy lássam, tényleg stimmel-e a dolog. Stimmelt.
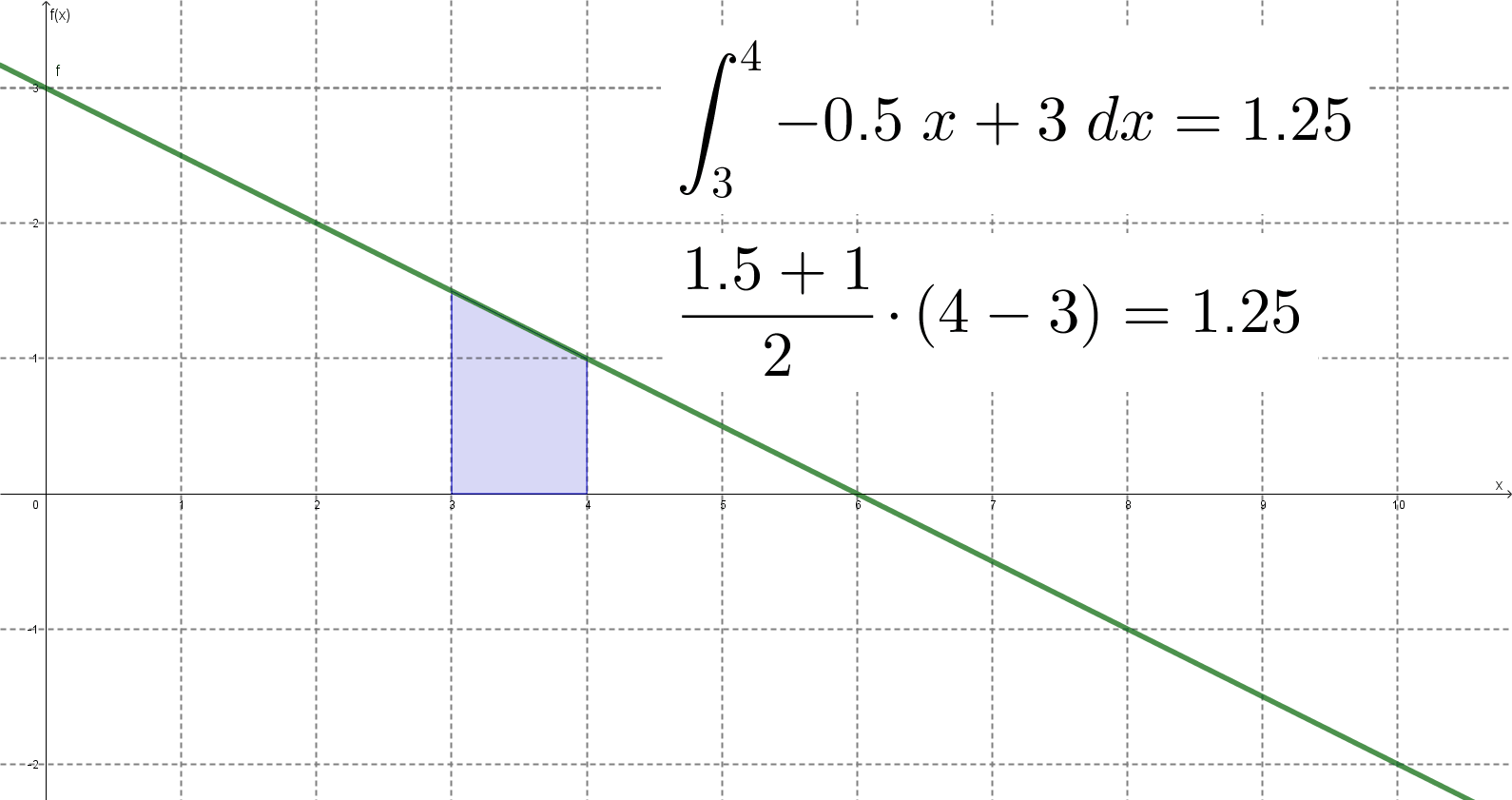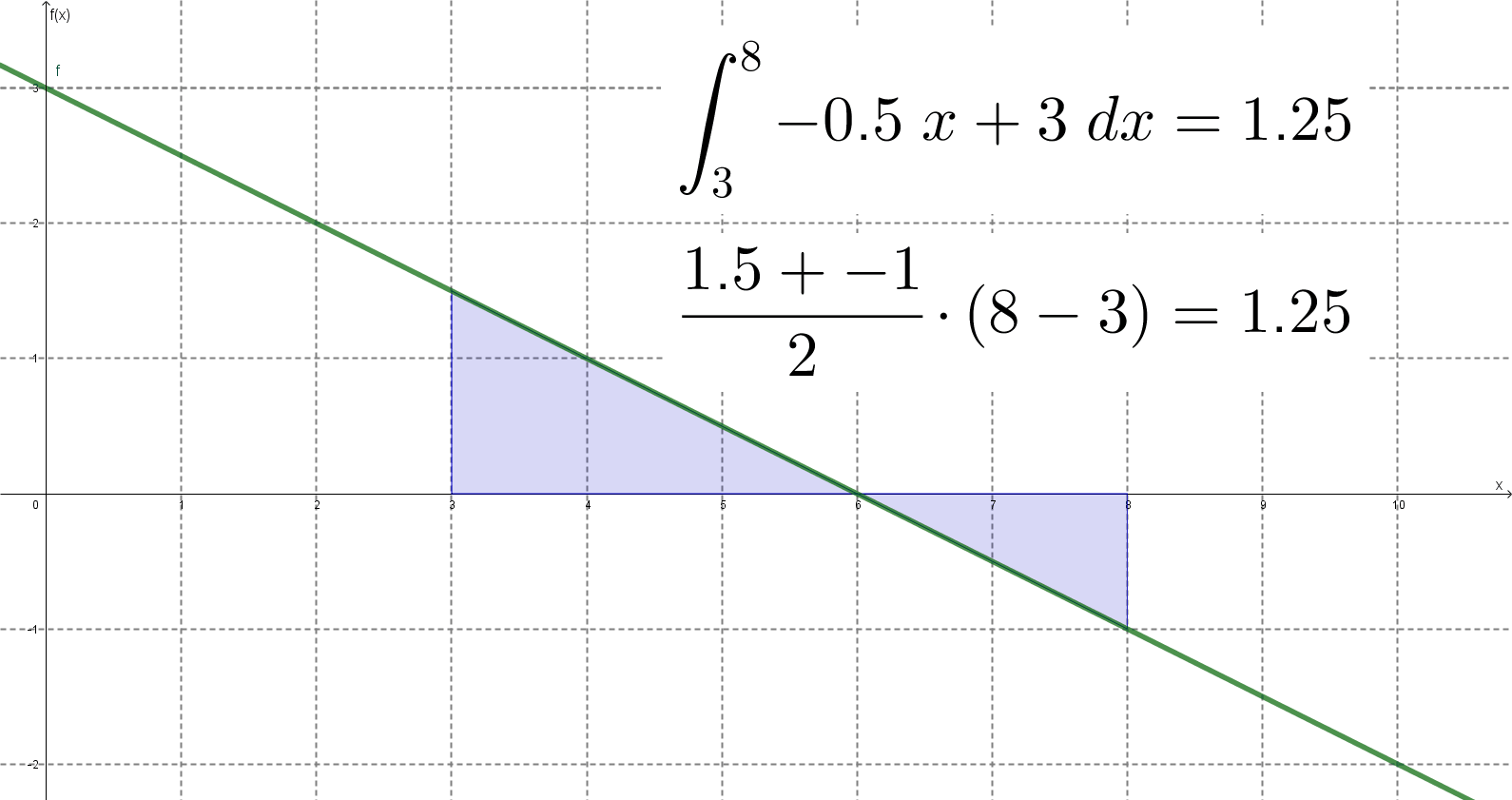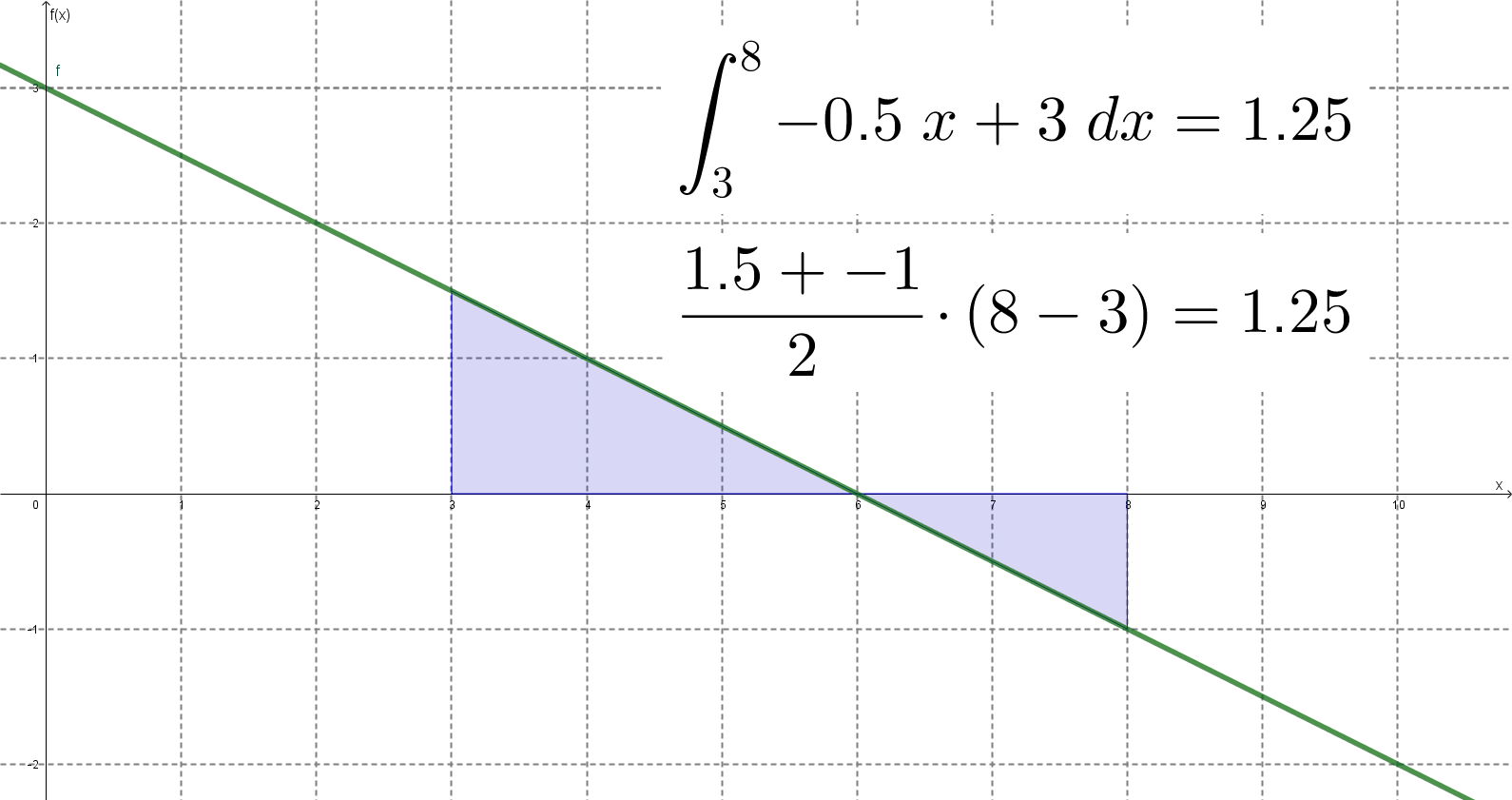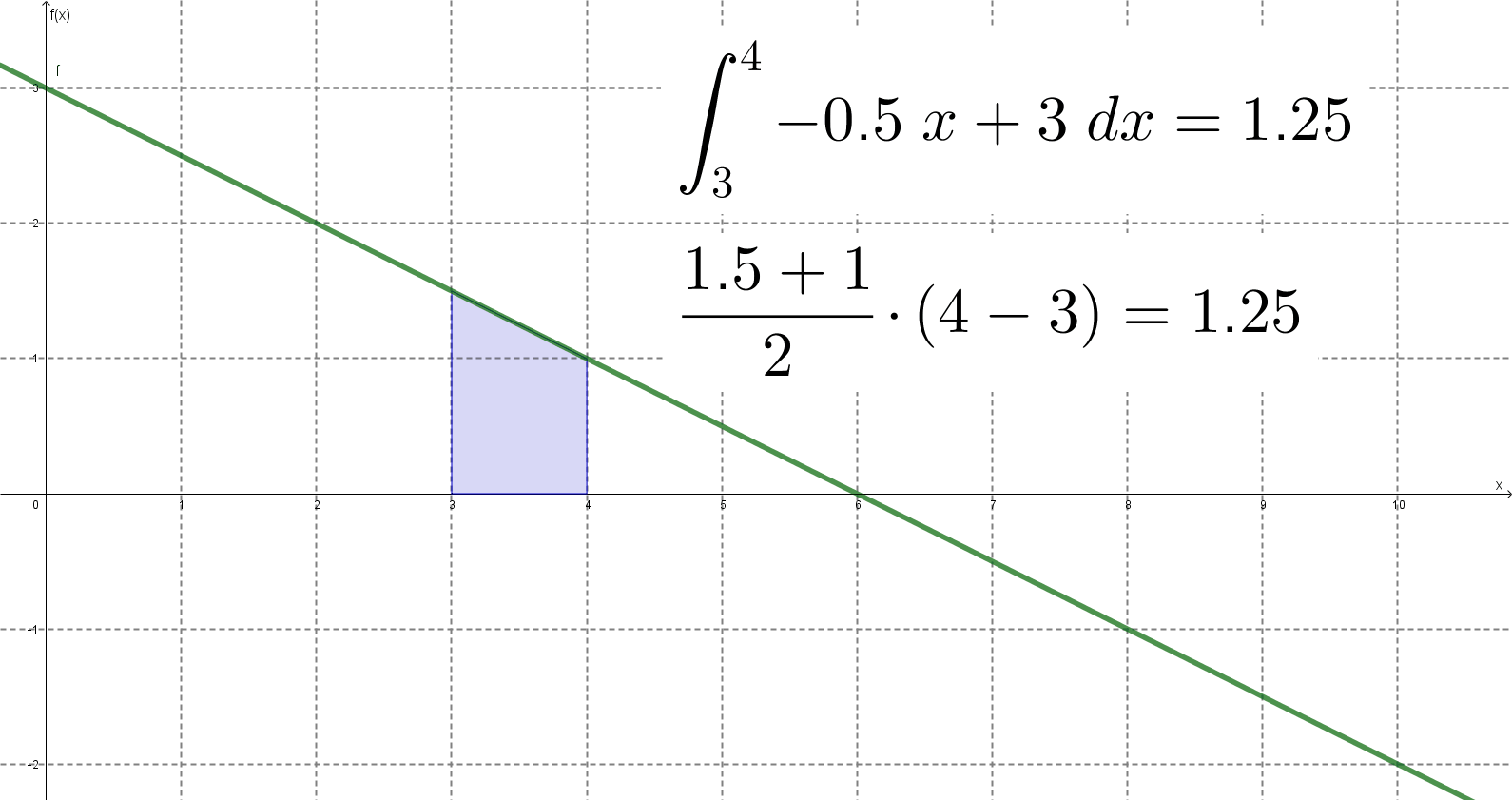
A módszer tehát általános érvényűnek látszott, úgyhogy megpróbáltam általános bizonyítást találni rá. Erre jutottam:
Tétel
Ha adott az f lineáris függvény, akkor a következő összefüggés érvényes:
Bizonyítás
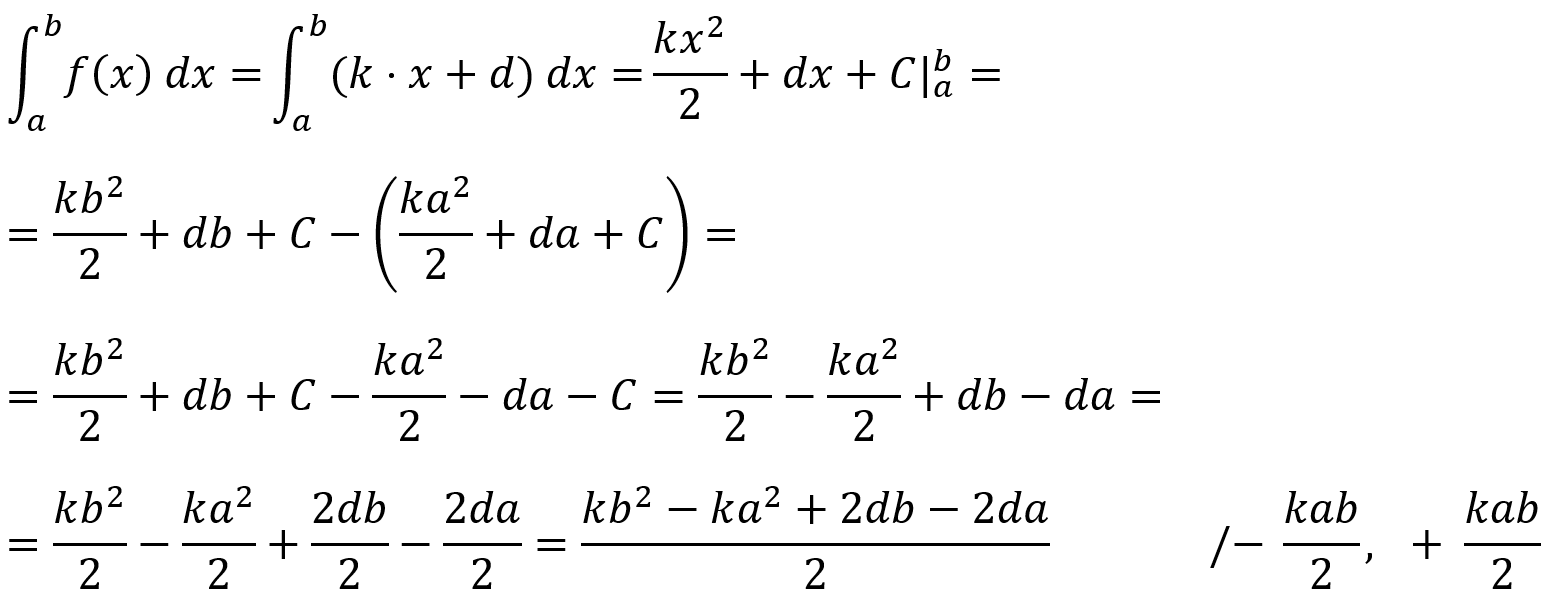
Így utólag azt mondom, hogy ez az a fajta tétel, aminek a bizonyítását egyetemen már az elsőéveseknek feladják házi feladatnak Analízis II-ből, de nekem valahogy nem volt ismerős. Megkérdeztem két kollégát is, de ők sem emlékeztek erre az állításra korábbról.
A következő órán aztán beszéltünk a tételről. Azt mondtam, hogy a diáknak jár a plusz a felfedezésért, aki viszont be is tudja bizonyítani, az két pluszt kap. Voltak is próbálkozások, de nem jártak sikerrel. Végül aztán kinyomtattam a fenti bizonyítás német változatát és kitettem az osztály faliújságára a következő óra után.
Egyébként a felfedezőt és az osztályt általában (két kivételtől eltekintve) kevéssé érdekelte a bizonyítás. Az volt az érzésem, hogy ők ezt csak felesleges szőrszálhasogatásnak látják. Számukra az volt a fontos, hogy működik módszer és miután egyszer vagy kétszer a helyes eredményre vezetett, elkönyvelték, hogy ezentúl így is lehet számolni.
Ezt a szemléletet azonban nem lehet a szemükre vetni. Gimnáziumban kötelező a matematika, azoknak is, akik aztán egyáltalán nem vagy teljesen más irányba tanulnak tovább. Ehhez igazodik a tanterv és az érettségi anyag is: vannak ugyan elméletibb jellegű feladatok, de az, hogy valamit általánosan bizonyítani kell, ritka a tankönyvekben és az érettségin is. Az olyan feladatok vannak többségben, ahol egyedi, konkrét problémákat kell megoldani, mert ezek a többség számára könnyebben érthetők és könnyebben begyakorolhatók, mint az elvont bizonyítások. A társadalmi elvárásoknak is inkább ezek felelnek meg: a legtöbben valószínűleg úgy vannak vele, hogy ha már egyszer kötelező tárgy a matematika a középiskolában, akkor az órán kapjanak használható tudást a diákok és legyenek életközeliek feladatok.
Ezt mind alá is írom. Ezzel együtt az a véleményem, hogy matematikatanárként a többség jogos igényeinek kiszolgálása mellett nyitva kell hagyni a felfelé vezető ajtót is; néha bele kell menni legalább egy-egy kisebb bizonyításba, mert lehet, hogy pont ez kelti fel a mélyebb érdeklődést a matematika iránt. Különben is, nehéz négy vagy öt évig ellenállni a kísértésnek, hogy bizonyítást mutasson az ember az órán.
