Ezt a bejegyzést valahol Bregenz és Bécs között írom a vonaton. Szombat van, reggel háromnegyed nyolc; kb. egy órája vagyok úton hazafelé és ha minden jól megy, öt óra előtt tíz perccel Budapesten leszek. Itt most kezdődött a tavaszi szünet, és a húsvét utáni keddig tart.

A vonatom az indulás előtt

A szünet előtt még jutott pár dolog az utolsó napra: az 5A osztály dolgozatot írt tegnap, amit délután ki is javítottam; volt egy kisebb szerepem a szünet előtti misén a Marienbergben és este még bevittem a Kenguru-tesztek eredményét a rendszerbe, hogy ki lehessen értékelni őket.

Az 5A dolgozata hat oldal volt. Egy nagy része tesztkérdésekből állt, de mégis tartottam tőle, hogy nem mindenki lesz kész vele időre. Ez a félelmem aztán alaptalannak bizonyult, mert többen is voltak, akik a tervezett ötven perc helyett már fél óra után kész voltak, úgyhogy még egy bónuszkérdést is felírtam a táblára. A javításnál kiderült, hogy bár mindenki végigért az összes kérdésen, előfordult, hogy egy-egy feladatot nem tudtak megoldani. A jegyek között, mint rendesen, volt ilyen is, olyan is, de összességében jól sikerültek. Ez annak is köszönhető, hogy a legtöbben megcsinálták a feladatlapot, amit feltöltöttem az internetre. Ezt onnan tudom, hogy még csütörtökön, a dolgozatot megelőző órán megbeszéltük a feladatokat, és szinte mindenki képben volt, mindenkinek voltak kérdései, és volt, hogy még egymást is kijavították ebben-abban, szóval látszott, hogy készültek. A jegyek is ennek megfelelően alakultak, de előfordult pár esetben, hogy az egyébként jó tanuló diák jegyét lerontották figyelmetlenségből eredő hibák.

Részlet a dolgozatból

Tegnap három órám volt, ebből a harmadik a Marienbergben, az Aufbaulehrgangon. Mivel ez volt az utolsó óra a szünet előtt, úgy döntöttem, hogy matematikatörténeti órát csinálok. Egy dokumentumfilmet néztünk meg a Fermat-sejtésről és annak bizonyításáról. A Fermat-sejtés nagyjából a 1660-as évektől ismert a matematikában. A következőről van szó: mindenki ismeri a Pitagorasz-tétel, amely azt mondja ki, hogy egy derékszögű háromszögben a befogók négyzetek területösszege megegyezik az átfogóra négyzetének területével. Röviden: a^² + b^² = c^² (a hatványozást a ^ jellel jelölöm, mert a blog szerkesztőfelülete valamiért nem enged felső indexbe írni, még html kóddal sem), ahol a és b a befogók, c pedig az átfogó.

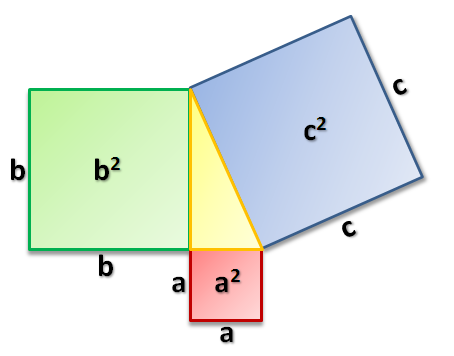
Illusztráció a Pitagorasz-tételhez

Pierre de Fermat az 1600-as évek első felében élt, és megsejtette, hogy ha a kitevő kettőnél nagyobb egész szám (és a, b, c szintén egész számok), akkor az egyenletnek nincs megoldása. Magyarul nincs olyan, hogy a^³ + b^³ = c^3 agy a^⁴ + b^⁴ = c^⁴ – hiába próbálunk bármilyen számot a, b és c helyére beírni; ha a hatványkitevő nagyobb, mint kettő, nem fog működni a dolog. Fermat Diophantosz Aritmetika c. könyvét olvasta, amikor lejegyezte a sejtést a könyv margójára. Hozzátette, hogy van erre egy igazán csodálatos bizonyítása, de a margó túl keskeny ahhoz, hogy leírja. A halála után aztán a fia kiadta Diophantosz Aritmetikáját az apja széljegyzeteivel együtt. Több hasonló sejtése is volt, amit a matematikusok az idők során vagy bebizonyítottak, vagy cáfoltak. Egyedül ez a sejtése állt ellen az általános bizonyítási kísérleteknek, egészen 1994 illetve 1995-ig, amikor Andrew Wilesnak sikerült megmutatnia, hogy Fermat sejtése helytálló volt. A film a bizonyítás kidolgozásáról és annak előzményeiről szólt. Csak angolul tudtam megszerezni, és német feliratot sem találtam hozzá, úgyhogy angolul néztük, angol felirattal. A film egyébként online is elérhető itt:

http://www.dailymotion.com/video/x223gx8_bbc-horizon-1996-fermat-s-last-theorem_shortfilms

Az óra után aztán mindenki átment a templomba, misére. A szertartáson én is szerepet kaptam, mert volt egy rész, ahol kilenc különböző nyelven elhangzott az, hogy Frieden ist möglich (a béke lehetséges). Magyarul én mondtam.